Para termos um entendimento suficientemente bom de algum assunto, não adianta estudarmos todas as ocorrências de todas as naturezas simultaneamente. O que os físicos fazem nestas situações é tentar achar um modelo simples e ir acrescentando os componentes aos poucos. No estudo de circuitos por exemplo, antes de entendermos como funciona um circuito integrado de televisão, precisamos entender a função de cada componente e seguir acrescentando um outro componente de cada vez, ou seja, primeiramente entendemos como se comporta um resistor, um capacitor e um indutor para posteriormente unirmos dois a dois e finalmente os três em apenas um circuito, denominamos estes circuitos de RL, RC, LC, e RLC. Neste texto entenderemos como funciona um circuito LC que contém de acordo com o que foi mencionado anteriormente um indutor e um capacitor. Vamos supor inicialmente que exista uma chave no circuito que permita ou não a passagem de corrente e que o capacitor está carregado inicialmente com uma carga q0. Em um instante inicial t=0, a chave é fechada, permitindo então a passagem de corrente através do circuito e a carga do capacitor começa então a fluir pelo circuito. Temos no circuito então uma corrente i=dQ/dt. Temos então que a queda de potencial no indutor é igual a Ldi/dt, e no capacitor é igual a Q/C. Através da Lei de Kirchhoff, podemos afirmar que Ldi/dt+Q/C=0. Utilizando noções de cálculo diferencial, sabemos que di/dt=d2Q/dt2. Substituindo esta última relação na equação do circuito, temos: d2Q/dt2=-Q/LC. Se chamarmos (de ![]() , temos a equação
, temos a equação ![]() . Denominamos (a frequência do circuito LC. Novamente utilizando cálculo diferencial, chegamos a um valor de Q=Acos(t+), onde A é a amplitude da carga, que é o valor máximo que a carga pode atingir e (é uma constante de fase que depende unicamente das condições iniciais do problema. Se considerarmos que a constante de fase é igual a zero temos que a carga neste circuito é dada por q0cost, uma vez que a amplitude da carga depende da carga inicial do capacitor, e derivando esta equação em relação ao tempo obtemos a corrente do circuito que é igual a i=-q0sent. Podemos perceber então que este circuito difere dos circuitos RC e RL já que ele não decai ou cresce exponencialmente, mas sim oscila. Isto acontece pois à medida que a carga no capacitor diminui, a energia armazenada no campo elétrico do capacitor se reduz. Esta energia não se perde, mas se transforma em energia magnética dentro do indutor, já que em torno deste circula uma corrente i que induz nele um campo magnético. Em um dado instante, toda energia elétrica do capacitor se esgota juntamente com sua carga. Temos então que a corrente no indutor agora é máxima e todo a energia do circuito está armazenada dentro do indutor sob forma de energia magnética.
. Denominamos (a frequência do circuito LC. Novamente utilizando cálculo diferencial, chegamos a um valor de Q=Acos(t+), onde A é a amplitude da carga, que é o valor máximo que a carga pode atingir e (é uma constante de fase que depende unicamente das condições iniciais do problema. Se considerarmos que a constante de fase é igual a zero temos que a carga neste circuito é dada por q0cost, uma vez que a amplitude da carga depende da carga inicial do capacitor, e derivando esta equação em relação ao tempo obtemos a corrente do circuito que é igual a i=-q0sent. Podemos perceber então que este circuito difere dos circuitos RC e RL já que ele não decai ou cresce exponencialmente, mas sim oscila. Isto acontece pois à medida que a carga no capacitor diminui, a energia armazenada no campo elétrico do capacitor se reduz. Esta energia não se perde, mas se transforma em energia magnética dentro do indutor, já que em torno deste circula uma corrente i que induz nele um campo magnético. Em um dado instante, toda energia elétrica do capacitor se esgota juntamente com sua carga. Temos então que a corrente no indutor agora é máxima e todo a energia do circuito está armazenada dentro do indutor sob forma de energia magnética.
Esta corrente flui pelo circuito e começa a realimentar o capacitor, aumentando assim o seu campo elétrico e diminuindo o campo magnético dentro do indutor. Agora o capacitor adquire carga máxima, porém a polarização de seu campo elétrico está invertida, e a carga começa a fluir no sentido contrário. Analisando as energias contidas em um circuito LC, vemos que a energia eletrostática do capacitor é dada por U=½ QV=Q2/2C. Substituindo nesta equação a função Q(t) obtida por nós anteriormente, temos U(t)=q02cos2t/2C. A energia magnética deste sistema é dada por U=½ Li2. Substituindo nesta equação a função i(t), temos U(t)=½ L2q02sen2t. Vemos que ora toda a energia se concentra no indutor, ora no capacitor, no entanto a energia total do sistema é dada sempre pela soma das duas, que é constante e igual a q02/2C.
Circuito RC
Quando estudamos qualquer assunto, tentamos dividi-lo em suas partes mais importantes e estudá-las separadamente dando a elas a devida atenção. Este é o caso do circuito RC que é um caso particular de um circuito elétrico contendo apenas uma resistência e um capacitor. Podemos pensar então nesses dois componentes ligados através de seus terminais e uma chave que pode permitir ou não a passagem de corrente no circuito. Admitindo inicialmente que a chave está aberta e não há passagem de corrente e o capacitor está carregado com uma determinada carga Q, vamos analisar o que vai acontecer quando a chave for fechada e possibilitar a passagem de corrente: Sabemos que a diferença de potencial entre os terminais do capacitor é dada por V0=Q0/C, onde Q0 é a carga inicial do capacitor e C sua capacitância. No instante t=0 fechamos a chave e a corrente começa a fluir através do resistor. A corrente inicial que passa pela resistência é igual a I0=V0/R. A medida que a corrente flui pelo circuito, a carga no capacitor decresce numa taxa igual a I=-Q/t, onde I é a corrente do circuito, e o sinal negativo aparece por se tratar de um caso de descarga do capacitor. Através da utilização da Primeira Lei de Kirchhoff, sabemos que o potencial no resistor é igual ao potencial no capacitor, obtemos então RI=Q/C. Podemos aplicar agora um pouco de cálculo diferencial e obter -R dQ/dt =Q/C. Resolvendo esta equação diferencial obtemos que a função Q dependente do tempo é igual a Q(t)=Q0e-t/RC. A letra e corresponde ao valor de 2,71828..., e é um número irracional com propriedades notáveis que são estudadas em um curso de cálculo. Ao analisarmos nossa equação vemos que Q0 é uma constante e depende da carga inicial do capacitor, t é o tempo e o produto RC é a chamada constante de tempo, e é este produto que determina qual é o tempo total de descarga do capacitor. Analisando esta constante percebemos que quanto maior for o produto RC maior será o tempo necessário para a descarga do capacitor e quanto menor o produto, menor será o tempo de descarga. Utilizando novamente o cálculo diferencial obtemos a função que governa a corrente: I(t)=I0e-t/RC. Vemos que analogamente à carga, a corrente cai exponencialmente com o tempo. Podemos analisar agora o que vai acontecer para um circuito RC conectado a uma bateria e com o capacitor descarregado. Ao fecharmos a chave, temos novamente pela Lei de Kirchhoff que o potencial da bateria mais o potencial no capacitor são iguais a zero. Neste caso temos então que I=dQ/dt, sem o sinal negativo, pois estamos agora lidando com o processo de carga do capacitor. Resolvendo novamente a equação diferencial obtemos que para o carregamento do capacitor Q(t)=CV(1- e-t/RC) e I(t)=(V/R) e-t/RC.
Portanto para o instante t=0 a carga no capacitor é igual a zero e a corrente que passa por ele é igual a V/R. À medida que o tempo passa, a carga no capacitor começa a aumentar e o fluxo de corrente começa a diminuir. Isto pode ser compreendido se pensarmos que o capacitor começa a funcionar como uma antibateria, já que ele começa a acumular cargas entre suas placas, e estas cargas estão dispostas no sentido contrário do sentido da bateria. O que acontece então é que quando o capacitor está completamente carregado, ele tem a mesma carga da bateria, só que a corrente por ele gerada está no sentido contrário, de forma que as correntes se cancelam, como era de se esperar.
Circuito RL
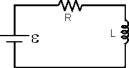
Sempre que aparece uma nova ideia ou uma nova teoria, os físicos tentam de toda a forma torná-la mais prática e mais simples de ser compreendida. É isto o que acontece quando estudamos um circuito RL, que é um caso particular de circuito, onde apenas existem dois componentes: O resistor e o indutor. Quando estudamos a Lei de Ohm, podemos perceber que a função de um resistor é dissipar a corrente elétrica, transformando parte dela em energia térmica. A função de um indutor é analisada quando se estuda a Lei de Faraday. Vemos então que o indutor funciona como uma inércia de um circuito, o que impede quedas ou aumentos bruscos de corrente. Dentro de um circuito, a resistência consiste geralmente de um determinado material que dificulta a passagem de corrente e o indutor é um solenóide ou uma bobina, que consistem em um fio condutor enrolado muitas vezes. Vamos considerar agora uma circuito RL, que possui uma bateria, uma chave que permite a passagem de corrente ou não, uma resistência e um indutor. Ao estudar os efeitos da auto-indutância de um sistema, vemos que a função de um indutor é de brecar a corrente que passa por ele gerando uma corrente de sentido oposto, então consideramos que a chave do circuito está aberta e é fechada no instante t=0 quando se inicia a passagem de corrente pelo sistema. Quando a corrente chega ao indutor, um potencial aparece dificultando a passagem de corrente, e este potencial é igual a =Ldi/dt, onde L é a indutância do indutor, e di/dt é a forma diferencial de se expressar a variação da corrente no tempo. Temos que lembrar ainda que este potencial sempre vai estar contrário à corrente que o atravessa de acordo com a Lei de Lenz. Sabemos também que a queda de potencial no resistor R é, pela Lei de Ohm, igual a Ri. Utilizando as regras de Kirchhoff para este circuito, podemos afirmar que o potencial V da bateria é igual a V=Ri+Ldi/dt. Para um instante muito próximo do instante inicial t=0, sabemos que a corrente é zero em todo o circuito, então a taxa de variação de corrente pelo tempo é dada por di/dt=V/L. Após a passagem de um pequeno intervalo de tempo, a corrente já flui pelo circuito e a variação temporal da corrente torna-se di/dt=V/L-iR/L. Quando a taxa de variação de corrente é igual a zero, sabemos então que a corrente no circuito atingiu seu valor máximo: imax=V/R. Vamos analisar a equação anteriormente citada do circuito e descobrir qual é o tempo necessário para que a corrente atinja seu valor final: A resolução da equação diferencial V=Ri+Ldi/dt através de processos de cálculo diferencial nos dá que ![]() . Nesta equação, chamamos a constante tc de constante de tempo, de forma que ela seja igual a R/L, e é esta a divisão que determina o intervalo de tempo necessário para que o circuito atinja sua corrente máxima.
. Nesta equação, chamamos a constante tc de constante de tempo, de forma que ela seja igual a R/L, e é esta a divisão que determina o intervalo de tempo necessário para que o circuito atinja sua corrente máxima.
Se considerarmos que temos agora um circuito no qual podemos remover a bateria após um certo instante, a nossa equação do circuito se reduz a: iR+ldi/dt=0 (di/dt=-Ri/L. Resolvendo esta equação, obtemos que ![]() , e neste caso vemos que a corrente, com o passar do tempo, tende a diminuir sempre e vai para zero para tempos decorridos muito grandes.
, e neste caso vemos que a corrente, com o passar do tempo, tende a diminuir sempre e vai para zero para tempos decorridos muito grandes.
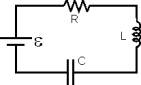
Vamos ver agora o estudo de um circuito RLC, que é basicamente um circuito que contém um resistor, um indutor e um capacitor. Vamos supor então que haja uma chave neste circuito que permita a passagem ou não de corrente e vamos supor também que o capacitor esteja carregado com uma carga inicial q0. Inicialmente a chave está aberta e não há passagem de corrente pelo circuito, no instante t=0 a chave é fechada e o capacitor começa o seu processo de descarga devido à diferença de potencial entre suas placas. Pela Lei de Kirchhoff, sabemos que a soma de todas as quedas de potencial em todos os elementos do circuito deve ser igual a zero, logo: ![]() . Sabemos que i=dQ/dt, e substituindo este valor na equação obtemos
. Sabemos que i=dQ/dt, e substituindo este valor na equação obtemos ![]() . Esta equação é idêntica a uma equação de um oscilador amortecido estudado em ondas. Um oscilador amortecido pode ser imaginado como um sistema massa mola mergulhado em uma substância viscosa como um óleo. Quando consideramos um sistema massa-mola, ele oscila indefinidamente se considerarmos desprezíveis todos os atritos, no entanto se colocarmos este sistema dentro do óleo, o atrito viscoso entre o sistema e o óleo, produzirá calor e diminuirá a energia cinética do sistema, que oscilará cada vez com amplitudes menores. Antes de se estudar o circuito RLC, estudamos em separado os circuitos RL, RC e LC e percebemos que nos circuitos RL e RC, ocorre ou uma queda ou uma subida exponencial na corrente enquanto em um circuito LC, a corrente oscila de um lado para o outro. Vemos então que a mistura RLC resulta em um circuito oscilante que cai exponencialmente. Vamos agora analisar este circuito energeticamente: Multiplicando todos os termos desta equação por i, temos:
. Esta equação é idêntica a uma equação de um oscilador amortecido estudado em ondas. Um oscilador amortecido pode ser imaginado como um sistema massa mola mergulhado em uma substância viscosa como um óleo. Quando consideramos um sistema massa-mola, ele oscila indefinidamente se considerarmos desprezíveis todos os atritos, no entanto se colocarmos este sistema dentro do óleo, o atrito viscoso entre o sistema e o óleo, produzirá calor e diminuirá a energia cinética do sistema, que oscilará cada vez com amplitudes menores. Antes de se estudar o circuito RLC, estudamos em separado os circuitos RL, RC e LC e percebemos que nos circuitos RL e RC, ocorre ou uma queda ou uma subida exponencial na corrente enquanto em um circuito LC, a corrente oscila de um lado para o outro. Vemos então que a mistura RLC resulta em um circuito oscilante que cai exponencialmente. Vamos agora analisar este circuito energeticamente: Multiplicando todos os termos desta equação por i, temos: ![]() . O primeiro termo desta equação nos indica qual é a quantidade de energia magnética que é injetada ou retirada do indutor, de forma que podemos obter um valor positivo ou um negativo, dependendo do sentido do fluxo de energia. No segundo termos da equação, temos o valor da energia elétrica do capacitor, cujo sinal também depende do sentido do fluxo de energia. Já para o terceiro termo, temos a energia dissipada no resistor por efeito Joule, e este valor é sempre positivo. Como já vimos em um circuito LC, a soma das energias elétrica e magnética é sempre constante, porém no caso RLC, há uma dissipação da energia no resistor, então a quantidade oscilante de energia entre o indutor e o capacitor tem sua amplitude sempre reduzida com o passar do tempo. O modo que a corrente cai com o tempo depende das relações entre os termos R2 e 4L/C, pois são estes termos que definem a curva na equação diferencial.
. O primeiro termo desta equação nos indica qual é a quantidade de energia magnética que é injetada ou retirada do indutor, de forma que podemos obter um valor positivo ou um negativo, dependendo do sentido do fluxo de energia. No segundo termos da equação, temos o valor da energia elétrica do capacitor, cujo sinal também depende do sentido do fluxo de energia. Já para o terceiro termo, temos a energia dissipada no resistor por efeito Joule, e este valor é sempre positivo. Como já vimos em um circuito LC, a soma das energias elétrica e magnética é sempre constante, porém no caso RLC, há uma dissipação da energia no resistor, então a quantidade oscilante de energia entre o indutor e o capacitor tem sua amplitude sempre reduzida com o passar do tempo. O modo que a corrente cai com o tempo depende das relações entre os termos R2 e 4L/C, pois são estes termos que definem a curva na equação diferencial.
O caso em que R2<4LC, ocorre um fenômeno denominado amortecimento sub-crítico, e a corrente vai oscilando e diminui lentamente. Para o caso em que R2=4LC, temos o amortecimento crítico, e para este caso não há oscilação e a carga no capacitor decai continuamente e tende a zero em tempos grandes. Para o caso em que R2>4LC, temos o amortecimento super-crítico, e como a dissipação no resistor é muito grande, a carga no capacitor cai exponencialmente e rapidamente.
|
|
|
|
| Circuitos enviados por Vitória de Queiros | ||