1 – Definição:
Dados dois pontos fixos F1 e F2 de um plano, tais que a distancia entre estes pontos seja igual a 2c > 0, denomina-se elipse, à curva plana cuja soma das distancias de cada um de seus pontos P à estes pontos fixos F1 e F2 é igual a um valor constante 2a , onde a > c.
Assim é que temos por definição:
PF1 + PF2 = 2 a
Os pontos F1 e F2 são denominados focos e a distancia F1F2 é conhecida com distancia focal da elipse.
O quociente c/a é conhecido como excentricidade da elipse.
Como, por definição, a > c, podemos afirmar que a excentricidade de uma elipse é um número positivo menor que a unidade.
2 – Equação reduzida da elipse de eixo maior horizontal e centro na origem (0,0).
Seja P(x, y) um ponto qualquer de uma elipse e sejam F1(c,0) e F2(-c,0) os seus focos. Sendo 2a o valor constante com c < a, como vimos acima, podemos escrever:
PF1 + PF2 = 2.a
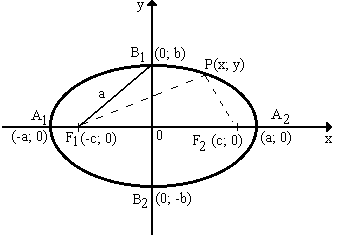
onde o eixo A1A2 de medida 2a, é denominado eixo maior da elipse e o eixo B1B2 de medida 2b, é denominado eixo menor da elipse.
Usando a fórmula da distancia entre dois pontos, poderemos escrever:
![]()
Observe que x – (-c) = x + c.
Quadrando a expressão acima, vem:
![]()
Com bastante paciência , desenvolvendo a expressão acima e fazendo a2 – c2 = b2 , a expressão acima depois de desenvolvida e simplificada, chegará a:
b2.x2 + a2.y2 = a2.b2
Dividindo agora, ambos os membros por a2b2 vem finalmente:
![]()
que é a equação da elipse de eixo maior horizontal e centro na origem (0,0).
Notas:
1) como a2 – c2 = b2 , é válido que: a2 - b2 = c2, onde c é a abcissa de um dos focos da elipse.
2) como a excentricidade e da elipse é dada por e = c/a , no caso extremo de termos b = a, a curva não será uma elipse e sim, uma circunferência, de excentricidade nula, uma vez que sendo b = a resulta c = 0 e, portanto e = c/a = 0/a = 0.
3) o ponto (0,0) é o centro da elipse.
4) se o eixo maior da elipse estiver no eixo dos y e o eixo menor estiver no eixo dos x, a equação da elipse de centro na origem (0,0) passa a ser:
![]()
EXERCÍCIOS RESOLVIDOS E PROPOSTOS
1 – Determine a excentricidade da elipse de equação 16x2 + 25y2 – 400 = 0.
SOLUÇÃO: Temos: 16x2 + 25y2 = 400. Observe que a equação da elipse não está na forma reduzida. Vamos dividir ambos os membro por 400. Fica então:
![]()
Portanto, a2 = 25 e b2 = 16. Daí, vem: a = 5 e b = 4.
Como a2 = b2 + c2 , vem substituindo e efetuando, que c = 3
Portanto a excentricidade e será igual a : e = c/a = 3/5 = 0,60
Resposta: 3/5 ou 0,60.
2 – CESCEA 1969 – Determine as coordenadas dos focos da elipse de equação
9x2 + 25y2 = 225.
SOLUÇÃO: dividindo ambos os membros por 225, vem:
![]()
Daí, vem que: a2=25 e b2=9, de onde deduzimos: a = 5 e b = 3.
Portanto, como a2 = b2 + c2, vem que c = 4.
Portanto, as coordenadas dos focos são: F1(4,0) e F2(-4,0).
3 – Determine a distancia focal da elipse 9x2 +25y2 – 225 =0.
SOLUÇÃO: a elipse é a do problema anterior. Portanto a distancia focal ou seja, a distancia entre os focos da elipse será:
D = 4 – (- 4) = 8 u.c (u.c. = unidades de comprimento).
4 – Calcular a distancia focal e a excentricidade da elipse 25x2 + 169y2 = 4225.
Resposta: e = 12/13 e df = 2c = 24.
5 – Determinar a equação da elipse com centro na origem, que passa pelo ponto P(1,1) e tem um foco F(-Ö 6 /2, 0).
Resposta: x2 + 2y2 = 3.