Trigonometria, Cosseno da diferença de arcos

Dedução da fórmula

Considere a figura abaixo que representa uma circunferência trigonométrica (centro na origem O(0,0) e raio unitário). Sejam a e b dois arcos trigonométricos com a > b.

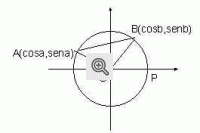Temos o arco PB de medida b e o arco PA de medida a. Nestas condições, podemos concluir que o arco BA tem medida a - b.
Pelo teorema dos cossenos, sabemos que em qualquer triângulo, o quadrado da medida de um lado é igual à soma dos quadrados das medidas dos outros dois lados, menos o dobro do produto desses lados, pelo cosseno do ângulo que eles formam. 

Assim, na figura acima, poderemos escrever, pelo teorema dos cossenos, para o triângulo OAB:
AB² = OB² + OA² - 2. OB . OA . cos(a - b). (Equação 1)
Ora, OB = OA = 1 (raio do círculo trigonométrico, portanto, unitário).
AB = distancia entre os pontos A(cosa,sena) e B(cosb,senb).
Já vimos nesta página, a fórmula da distancia entre dois pontos; se você não se lembra, revise os textos sobre Geometria Analítica .
Assim, substituindo os elementos conhecidos na fórmula acima (equação 1), vem:
(cosa - cosb)² + (sena - senb)² = 1² + 1² - 2.1.1.cos(a -b)
Desenvolvendo, vem:
cos²a - 2.cosa.cosb + cos²b + sen²a - 2.sena.senb + sen²b = 2 - 2cos(a - b)
Lembrando que cos²a + sen²a = cos²b + sen²b = 1 (Relação Fundamental da Trigonometria), vem, substituindo:
1 + 1 - 2cosacosb - 2senasenb = 2 - 2cos(a - b)
Simplificando, fica:
-2[cosacosb + senasenb] = -2.cos(a - b)
Donde finalmente podemos escrever a fórmula do cosseno da diferença de dois arcos a e b:

cos(a - b) = cosa . cosb + sena . senb

Exemplo: cos(x - 90º) = cosx . cos90º + senx . sen90º
Ora, como já sabemos que cos90º = 0 e sen90º = 1, substituindo, vem finalmente:

cos(x - 90º) = senx.

Se fizermos a = 0º na fórmula do cosseno da diferença, teremos:
cos(0 - b) = cos0 . cosb + sen0 . senb
E como sabemos que cos0 = 1 e sen0 = 0, substituindo, fica:

cos(- b) = cosb

Portanto:
cos( - 60º ) = cos60º = 1/2, cos( - 90º) = cos90º = 0, cos ( -180º) = cos 180º = -1, etc.
Se considerarmos a função y = cosx , como cos( - x ) = cosx , diremos então que a função cosseno é uma função par. Reveja o capítulo de funções.

Para finalizar, tente simplificar a seguinte expressão:
y = cos(x - 90º) - cos(x - 270º).
Resposta: 2senx