Balística é a ciência que se preocupa em estudar o movimento de corpos lançados ao ar livre, o que geralmente está relacionado ao disparo de projéteis por uma arma de fogo. Ao se estudar um projétil disparado por uma arma de fogo, pode-se separar seu movimento em três partes distintas: a balística interior, balística exterior e a balística terminal. A balística interior fica encarregada de estudar o que ocorre desde o momento do disparo até o instante em que o projétil abandona a arma. Este estudo fica baseado então na temperatura, volume e pressão dos gases no interior da arma durante a explosão do material combustível, assim como também se baseia no formato da arma e do projétil. Dependendo da quantidade utilizada de pólvora, deve-se ser estudado qual o material utilizado para a construção da arma e do projétil para evitar explosões desagradáveis.
A construção do cano interno da arma também tem de ser bem projetada. Grandes desenvolvimentos da balística interior foram realizados por Benjamin Robins, um engenheiro que realizou diversos experimentos nesta área no século XVIII. A balística exterior trata de estudar o que ocorre a partir do instante em que o projétil abandona a arma e o instante em que este atinge o alvo. Neste estudo entra a aerodinâmica, preocupada em estudar qual é a relação entre o movimento do projétil e o ar que o envolve. Calibre, formato, massa, velocidade inicial e rotação são fatores determinantes para a construção de um projétil com grande poder de destruição. Da simples análise física do assunto utilizando energia, podemos deduzir que a massa e a velocidade são muito importantes no desenvolvimento de uma arma e de um projétil, já que a energia cinética de um corpo é igual a Ec=½ mv2, e como a energia que será transmitida ao alvo será igual à energia cinética, a maximização desta permitirá um melhor resultado. Um dos motivos de controvérsia do passado estava relacionado com a trajetória dos projéteis.
Antes de Galileu, acreditava-se que a trajetória descrita por um projétil era retilínea, porém Galileu e Newton demonstraram que a trajetória de qualquer corpo sob ação da gravidade era parabólica. Os métodos utilizados para a medição da velocidade dos projéteis eram variados, e podiam ser feitos através da medição do momento deles ou então da distância percorrida entre dois pontos em um intervalo de tempo. O primeiro método era feito utilizando-se para isto um pêndulo balístico, que consistia em um anteparo pendurado em um teto. O projétil acertava então este anteparo e o deslocava. O ângulo de deslocamento era medido e sabia-se então qual era o momento transferido pelo projétil para o corpo, e através da fórmula para o momento, Q=mv, achamos facilmente o valor da velocidade. A balística terminal se encarrega de estudar o que ocorre no momento do impacto do projétil com o alvo. 0 estudo de balística terminal envolve muitas formas empíricas, porém estudos teóricos são realizados também para maximizar a penetração, permitir ou não a fragmentação do projétil ao atingir o alvo, a utilização ou não de apetrechos explosivos nos extremos do projétil, aumentando desta forma sua capacidade de destruição, etc.
Nos últimos anos, o estudo da balística têm obtidos grandes êxitos, já que o desenvolvimento de fotografias de alta- velocidade e do estroboscópio têm permitido o estudo aprofundado da movimentação de projéteis desde o momento em que são disparados até o instante em que atingem o alvo. Estes estudos são feitos através da inclusão destes dados em supercomputadores que permitem a otimização de armas e projéteis.
Lançamento de Projétil
Uma partícula é lançada com velocidade inicial v0, segundo um ângulo ![]() em relação ao eixo horizontal (lançamento oblíquo), estando sob a ação da aceleração da gravidade, agindo verticalmente para baixo, impondo uma trajetória parabólica, resultante da composição de dois movimentos.
em relação ao eixo horizontal (lançamento oblíquo), estando sob a ação da aceleração da gravidade, agindo verticalmente para baixo, impondo uma trajetória parabólica, resultante da composição de dois movimentos.
Sendo a velocidade uma grandeza vetorial, podemos decompô-la segundo os eixos x e y, com o intuito de estudarmos os movimentos separadamente. Com respeito a vertical, tem-se o movimento uniformemente variado e movimento uniforme segundo o eixo horizontal, visto que a aceleração da gravidade sendo vertical, não tem componente nesta direção. Em termos das componentes da velocidade inicial, percebe-se que:
- a componente de v0, na direção do eixo x é dada pela equação (3.14)
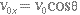
(3.14) - a componente de v0, na direção do eixo y é dada pela equação (3.15)
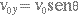
(3.15)
As equações de posição e velocidade estão agrupadas de acordo com o tipo de movimento, além de considerarmos a origem dos eixos de referência na posição de lançamento da partícula, o que faria de x0 e y0 valores nulos. Vamos às equações:
- movimento na direção x (MRU)
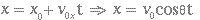
(3.16) - movimento na direção y (MUV)
Nossos resultados serão obtidos para uma referência positiva sendo considerada para cima e origem no ponto de lançamento. Os resultados são:
- Altura máxima ymax. Por Torricelli (3.19) e sabendo-se que vy é nulo,
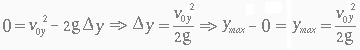 então, a altura máxima é dada pela equação (3.20)
então, a altura máxima é dada pela equação (3.20)

(3.20) - Tempo de subida ts. Partindo-se da equação de velocidade (3.18) e sabendo-se que vy é nulo, encontra-se para o tempo de subida, equação (3.21)

(3.21) - Alcance máximo R = xmax. O alcance é máximo quando o tempo t é igual ao tempo de queda tq. Sendo o tempo de queda o dobro do tempo de subida, pois y = 0 e usando-se a equação de movimento (3.17)
obtém-se o tempo de queda
e substituindo-se o tempo de queda na equação de movimento horizontal (3.16) encontra-se rearrumando tem-se para xmax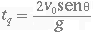
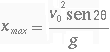
(3.22) - y em função de x Devemos isolar o tempo na equação de movimento para o eixo x (3.16) e substitui-lo na equação de movimento para o eixo y (3.17) encontrando-se
de onde se tem y em função de x mostrado na equação (3.23)
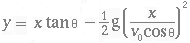
(3.23)
Links para simulações em Java
Simulador Balístico
Trajetória Balística
http://www.fisica.ufpb.br/prolicen/Cursos/Curso1/mr35lp.html