1 - Introdução
- Trigonometria: vocábulo criado em 1595 pelo matemático alemão Bartholomaus Pitiscus (1561-1613), do grego trigonon (triângulo) e metron (medida).
- É claro que Hiparco (astrônomo e matemático grego (190 a.C. - 125 a. C.), considerado o pai da Trigonometria, ainda não usava esta terminologia.
- A Astronomia foi a grande impulsionadora da Trigonometria.
- O desconhecimento dos números negativos, que se popularizou apenas no século XVII, dificultou o desenvolvimento da Trigonometria.
- O documento mais antigo conhecido sobre o assunto, data-se do século II d.C. e denominou-se Almagesto, de autoria de Ptolomeu. (Cláudius Ptolemaeus astrônomo grego (90 - 168).
Afirma-se que Ptolomeu deixou o planeta Terra aos 78 anos.
Este grande astrônomo grego acreditava que a Terra era o centro do Universo, ao redor da qual giravam Mercúrio, Lua, Vênus, Sol, Marte, Júpiter e Saturno, em órbitas que seriam círculos perfeitos! Sua concepção foi considerada como válida até o século XVI, quando Nicolau Copérnico (astrônomo polonês - 1473/1543) a substituiu pela teoria heliocêntrica (válida até hoje) e confirmada por Galileo Galilei (físico e astrônomo italiano - 1564/1642). - Por enquanto, vamos ver apenas a definição de círculo trigonométrico, após o resumo histórico supra. Nos próximos textos, cuidaremos de desenvolver o resumo da teoria.
Chama-se Círculo Trigonométrico, ao círculo orientado de raio unitário, cujo centro é a origem do sistema de coordenadas cartesianas, conforme figura a seguir.
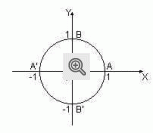O círculo trigonométrico é orientado positivamente no sentido ABA’B’A. O sentido AB’A’BA é considerado negativo. Assim, o arco AB (ângulo reto) mede 90º e o arco AB’ mede -90º . O arco ABA’ (ângulo raso) mede 180º ( ou p radianos) e o arco AB’A’ mede (-180º).
O arco de uma volta completa (ABA’B’A) mede 360º ;
O arco AB’A’BA mede( -360º), ou seja, é um arco negativo.
Já sabemos que 360º = 2p radianos.
Podemos na Trigonometria, considerar arcos de mais de uma volta.
Sabendo que uma volta equivale a 360º , podemos facilmente reduzir qualquer arco à primeira volta. Por exemplo, o arco de 12350º , para reduzi-lo à primeira volta, basta dividi-lo por 360º (para eliminar as voltas completas) e considerar o resto da divisão. Assim é que, 12350º dividido por 360º, resulta no quociente 34 e no resto 110º. Este valor 110º é então trigonométricamente equivalente ao arco de 12350º e é denominado sua menor determinação positiva.
Dois arcos trigonométricos são ditos côngruos, quando a diferença entre eles é um número múltiplo de 360º . Assim é que sendo x e y dois arcos trigonométricos, eles serão côngruos se e somente se x - y = k . 360º , onde k é um número inteiro.
Portanto, para descobrir se dois arcos são côngruos, basta verificar se a diferença entre eles é um múltiplo de 360º (ou 2p radianos, pois 2p rad = 360º).
Os arcos 2780º e 1700º , por exemplo são côngruos , pois
2780º - 1700º = 1080º e 1080º é divisível por 360º
(1080º / 360º = 3 , com resto nulo).
Exercício resolvido:
Quantos são os valores de m compreendidos entre 30 e 40, que tornam côngruos os arcos de medidas (4m+10).180º e (3m-2).180º ?
Solução:
Pela definição de arcos côngruos dada acima, deveremos ter:
(4m+10).180º - (3m-2).180º = k . 360º , onde k é um número inteiro.
720m + 1800 -[540m - 360] = k . 360
720m + 1800 - 540m + 360 = k . 360
180m + 2160 = k . 360
180m = k . 360 - 2160
m = 2k - 12
Mas, pelo enunciado, temos 30 < m < 40. Logo:
30 < 2k - 12 < 40
42 < 2k < 52
21 < k < 26 Þ k = 22, 23, 24 ou 25.
Existem 4 valores possíveis para k e, portanto, também 4 valores possíveis para m,
já que m = 2k - 12.
Resposta: m possui 4 (quatro) valores distintos.
Testes Verdadeiro - Falso
1 - Os arcos de 4200º e 3480º são côngruos
2 - Os arcos de (- 420º ) e 300º são côngruos.
3 - O arco de 10.002º pertence ao segundo quadrante.
4 - O arco de (- 200º) pertence ao segundo quadrante.
Gabarito:
1 - V
2 - V
3 - F
4 - V