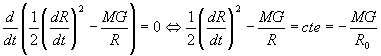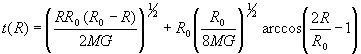Introdução Histórica
A expressão buraco negro foi adotada pela primeira vez pelo cientista norte-americano John Wheeler, em 1969, para descrever uma ideia surgida 200 anos antes. Em 1783 o professor de Cambridge John Michell escreveu um trabalho, onde disse que poderia haver uma estrela compacta com massa suficiente para que nem a luz pudesse escapar da atração gravitacional desta. Alguns anos depois, Laplace fez a mesma proposição, de forma independente, mas só a incluiu nas duas primeiras edições de seu livro O sistema do mundo.
Em 1928, Chandrasekhar embarcou para a Inglaterra para estudar com o astrônomo inglês Eddington, durante a viagem questionou como poderia uma estrela se sustentar contra sua própria gravidade quando acabasse seu combustível nuclear. Chandrasekhar calculou então que uma estrela com cerca de uma vez e meia a massa do Sol não seria capaz de se sustentar contra sua própria gravidade, esta é a massa limite de Chandrasekhar. Descoberta equivalente foi feita na mesma época pelo física russo Landau.
Para estrelas acima desta massa crítica, a previsão era de que elas se livrariam de parte de suas massas até estarem abaixo da massa limite, ou colapsariam em um ponto de densidade infinita; Eddington e outros cientistas não concordavam com isto. Chandrasekhar abandonou esta linha de pesquisa e se voltou ao estudo do movimento de aglomerados de estrelas.
O que ocorre com uma estrela com massa superior a massa limite, só ocorreu em 1939, quando Oppenheimer estudou o que aconteceria com estas estrelas pelo ponto de vista da relatividade geral; mas com a segunda guerra Oppenheimer se voltou ao projeto da bomba atômica.
Na década de 1960, a tecnologia permitiu aumento no número e na amplitude das observações astronômicas, revigorando interesse nas áreas da macroastronomia e cosmologia. O trabalho de Oppenheimer foi então redescoberto e continuado.
Relatividade Geral
A teoria da Relatividade Restrita ou Especial aplicava o princípio da relatividade a referenciais inerciais. Em 1916 Einstein ampliou sua teoria para incluir referenciais não inerciais, essa generalização é a teoria da Relatividade Geral. A seguir discutiremos alguns aspectos qualitativos desta teoria.
Um postulado da teoria geral da relatividade é o princípio da equivalência, que diz que nenhum experimento realizado localmente pode distinguir entre um referencial com aceleração constante e um referencial sob ação de um campo gravitacional também constante. Então um observador colocado em uma caixa fechada, não poderá saber se esta está em queda livre ou sendo acelerada com a mesma aceleração da gravidade em uma região com potencial gravitacional nulo (embora a força gravitacional exercida por um corpo nunca se anule, caindo com o inverso do quadrado da distância, podemos admitir que a força seja nula distante do corpo, pois neste caso ela tende a zero). Nos dois casos, um corpo abandonado pelo observador a uma altura do solo, terá o mesmo movimento. O princípio da equivalência está relacionado com a equivalência entre as massas gravitacionais e inerciais de um corpo. A massa inercial determina a resposta do corpo quando este está em um referencial inercial (velocidade constante) e a massa gravitacional determina a resposta do corpo quando em um campo gravitacional, como o movimento descrito nos dois casos é igual, os dois tipos de massa são equivalentes.
Para a teoria newtoniana, o espaço e o tempo eram grandezas independentes, já no ponto de vista da relatividade especial, estas grandezas estão interrelacionadas, de forma que os fenômenos ocorrem num espaço quadridimensional, o espaço-tempo.
Do ponto de vista da teoria newtoniana, a gravidade era uma força gerada pela massa dos corpos, para a relatividade especial a gravidade é resultado de uma deformação no espaço-tempo, devido as massas dos corpos contidos neste. Então a gravidade passa a ser um fator geométrico, a gravitação é considerada como uma curvatura no espaço-tempo quadridimensional.
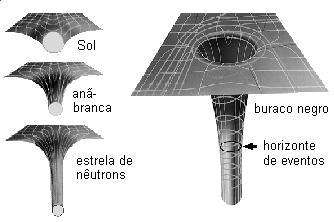 |
| ilustração mostrando a deformação no espaço-tempo causada pelo Sol, por uma anã branca, estrela de nêutrons e por um buraco negro. |
Considere o movimento da Terra em torno do Sol. O Sol é um corpo massivo que provoca uma distorção do espaço tempo ao seu redor, e a Terra se move ao longo da menor trajetória entre dois pontos no espaço curvo, tridimensionalmente, exergamos essa trajetória como uma elipse.
Esses efeitos de curvatura no espaço tempo são desprezíveis ao redor de pequenas massas, mas se tornam significativos ao redor de estrelas, por exemplo. A distorção que um buraco negro provoca no espaço-tempo é tão acentuada que faz com que nem a luz possa escapar dele.
Se fizermos o limite desta teoria para pequenas massas, obteremos a teoria da gravitação de Newton, que é suficiente para descrever movimentos como o dos planetas ao redor do Sol.
Evolução de uma estrela massiva (M>15M¤ )
A partir de uma nuvem de gás que se contrai, se forma a protoestrela. Quando a contração aumenta a pressão, gerando uma temperatura suficiente no núcleo da estrela para iniciar a queima do hidrogênio em hélio, dizemos que a estrela está na fase de sequência principal; nesta fase a contração é bem mais lenta. Quando todo o hidrogênio do núcleo já foi queimado em hélio, a estrela passa a queimar hélio em carbono, quando isso ocorre dizemos que a estrela saiu da fase de sequência principal. Quando todo o hélio do núcleo já foi queimado, a estrela passa a queimar carbono em silício ,magnésio, oxigênio e ferro. Quando o combustível nuclear da estrela acaba, ela colapsa, eliminando suas camadas externas em uma supernova; nesta explosão podem ser sintetizados elementos mais pesados. Desta explosão pode restar uma estrela de nêutrons ou um buraco negro.
Colapso de uma estrela
a equação do movimento de uma partícula da superfície da massa colapsando em queda livre é dada por:
![]()
cancelando m e multiplicando por dR/dt temos a expressão de conservação da energia:
onde R = R(t) e R0 é o raio da estrela antes da contração, isto é, R(t=0) = R0. A solução desta equação diferencial é dada por:
esta equação determina implicitamente o raio de um objeto durante o colapso em função do tempo.
Para determinar o tempo total do colapso, quando a estrela colapsa para um ponto, faremos R = 0
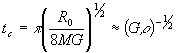
então o tempo total de colapso tc é dependente apenas da densidade média e não do raio.
Podemos escrever:
![]()
esta deverá ser a frequência de rotação de um corpo não estabilizado pela pressão interna (uma galáxia, por exemplo) para que não colapse.
Para uma estrela colapsante com massa menor que a massa de Chandrasekhar MC haverá um novo estado de equilíbrio. Se a massa for superior a MC e menor que 10.M¤ o colapso é acompanhado por ondas de choque que farão com que a estrela expulse massa, restando apenas a massa de uma estrela de nêutrons, isto provavelmente ocorre durante a explosão da estrela sob a forma de uma supernova. A massa de gás expelida ficará ao redor da estrela formando uma nebulosa.
Para uma estrela colapsante de massa M > ~ 5 M¤ nem a pressão dos nêutrons nem dos elétrons será suficiente para parar a contração e, de acordo com a teoria da gravitação de Newton, a estrela colapsará a um ponto de densidade infinita, uma singularidade. A relatividade geral confirma a previsão da teoria newtoniana.
Fonte: <http://www.geocities.com/CapeCanaveral/Launchpad/8602/astro/bn/bnhp.htm>
Algumas Noções de Gravitação para Aplicar aos Buracos Negros
Para que um corpo de massa m1 escape ao campo gravitacional de um corpo de massa m2 tem-se que a energia cinética de lançamento de m1 deve ser igual a sua energia potencial no infinito. Portanto:
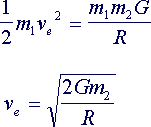
Eq. 1
onde Ve é a velocidade de escape, G é a constante gravitacional e R é o raio do corpo. Daí podemos tirar alguns resultados para corpos conhecidos: Para a Terra Ve = 11,2 km/s
Para o Sol Ve = 618 km/s
Para uma estrela de nêutrons Ve = 0,5c onde c = 300.000 km/s (a velocidade da luz).
O Efeito dos Buracos Negros Sobre a Radiação
O Raio de Schwarzschild e o Horizonte de Eventos
Partindo da equação 1 podemos substituir Ve por c (velocidade da luz) e isolar o raio. Dessa forma encontraremos o raio em que a velocidade de escape é igual à velocidade da luz. Este raio é denominado de Raio de Schwarzschild que delimita o Horizonte de Eventos.
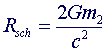
Eq. 2
Obs: Embora a dedução correta para o Raio de Schwarzschild a partir da eq.1 não seja rigorosa o suficiente, a dedução mais rigorosa, levando em consideração a teoria da relatividade, fornece o mesmo resultado. Esta fronteira é chamada de horizonte de eventos porque nenhuma informação sai de dentro dela. Qualquer corpo que assumir um tamanho menor do que o do seu horizonte de eventos irá colapsar a um ponto. O raio do horizonte de eventos determina ainda o raio da Esfera de Fótons (ver abaixo).
Na eq.2, observamos que o raio de Schwarzschild é proporcional à massa do corpo colapsado. Podemos calcular seu valor para diferentes massas.
Assim:
1. Para um corpo com a massa do Sol, temos que RSch = 3 km
2. Para corpos com duas Msolares, RSch = 6 km
3. Para a Terra, RSch = 8.9 x10-3 m ou 8.9 mm
A Esfera de Fótons A radiação eletromagnética que se encontra nas imediações de algum corpo massivo como uma estrela sofre uma forte atração do campo gravitacional da estrela de forma que a trajetória que a radiação toma é curvada na direção da estrela. Vamos supor agora, que pudéssemos nos posicionar a uma certa distância de um buraco negro com uma fonte luminosa que projete um feixe que possa ser direcionado para onde desejarmos. Vamos então nos posicionar a uma distância em que possamos notar melhor os efeitos de curvatura sobre a luz e ver o que acontece com o nosso feixe luminoso.
 |
| A esfera externa é a esfera de fótons e a interna, o horizonte de eventos. Acima, o cone de saída. |
Primeiro vamos projetar o feixe na direção radial ao buraco negro. Observaremos que o feixe continua a propagar-se perpendicularmente. Vamos ver, ainda, o que acontece ao feixe luminoso ao desviá-lo de um ângulo X da direção radial. Vemos que ele se curva devido ao efeito do campo gravitacional do buraco negro. E se inclinarmos mais ainda vamos ter um determinado ângulo Y maior que 90o no qual o feixe não escapa do campo gravitacional do buraco negro e entra em órbita. Se inclinarmos além desse ângulo Y o feixe cairá de volta no buraco negro.
Aproximando-nos ainda mais do buraco negro vamos observar que haverá uma certa distância em que a luz entra em órbita ao redor da estrela ao direcionarmos o feixe à 90o com a vertical. Neste momento estaremos sobre a chamada "Esfera de Fótons". Se inclinarmos o feixe de luz além desse ângulo ele cairá no buraco negro.
Se diminuirmos mais a distância até o buraco negro devemos ter ângulos menores do que 90° com a vertical nos quais o feixe entrará em órbita e a partir dos quais o feixe cairá. O ângulo de saída para o qual o feixe entra em órbita é chamado de ângulo de saída.
A esfera de fótons recebe este nome porque é nessa "esfera" que os fótons orbitam o buraco negro. Dessa forma se estivéssemos sobre a esfera de fótons olhando em uma direção qualquer perpendicular à vertical, veríamos sempre a nossa nuca.
Como encontrar um Buraco Negro
Não é possível observar um buraco negro diretamente porque ele não emite radiação. Entretanto, um buraco negro exerce força gravitacional sobre os corpos ao seu redor e graças a isso podemos detectá-lo. Um modo de detectar um candidato a buraco negro é procurá-lo em sistemas binários (duas estrelas que orbitam uma ao redor da outra) onde uma das componentes do sistema parece ser invisível e tenha massa maior do que 3-6 Msolares.
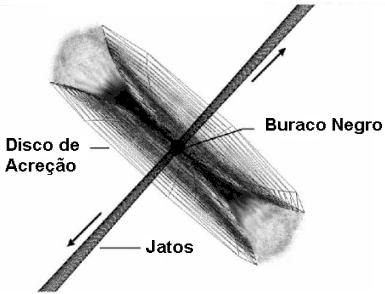 |
| Disco de acresção orbitando um Buraco Negro. |
Através do estudo da deflexão da órbita da estrela visível do sistema duplo pode-se descobrir a massa do objeto invisível e assim confrontar o resultado encontrado com o limite mínimo de massa para a existência de um buraco negro. Outro indício de que o sistema possa conter um buraco negro é a presença de um disco de acresção. Este se forma porque o buraco negro captura matéria da companheira que é "engolida" através de um disco no qual a matéria pode perder o excesso de momentum angular via um processo de fricção que aquece a matéria capturada a 107 K. Este aquecimento provoca uma forte emissão de raios-X.
As emissões fortes de raios-X podem vir de outras fontes. Assim devem existir evidências mais específicas de que estes raios sejam mesmo originados em um disco de acresção aquecido por fricção, orbitando um buraco negro. Para que um candidato seja realmente um disco de acresção ele deve ter dimensões pequenas (da ordem de dias-luz) para que seja coerente com o modelo proposto. Deste modo deve-se procurar fontes de raios-X com período de variação da emissão da ordem de dias-luz.
Outro indício da presença de discos de acresção é o efeito Doppler na luz emitida (observável se o disco emitir radiação em uma linha de emissão de comprimento de onda ao conhecido). Se o disco de acresção estiver inclinado em relação ao observador, este observador verá um lado do disco se "aproximar" com uma certa velocidade (que é muito alta para um disco de acresção orbitando um buraco negro) e verá o outro lado do disco se afastar com a mesma velocidade.
Algumas respostas para suas dúvidas sobre buracos negros
[P]O que é um buraco negro?
De forma muito simplista, um buraco negro é uma região do espaço que contém tanta massa concentrada que nenhum objeto consegue escapar de sua atração gravitacional. Como a melhor teoria gravitacional no momento ainda é a Teoria da Relatividade Geral de Einstein, somos obrigados a mergulhar em alguns dos resultados preditos por essa teoria para entender os detalhes de um buraco negro, mas vamos começar devagar, pensando sobre a gravidade em circunstâncias relativamente simples.
Suponha que você está na superfície de um planeta. Você atira uma pedra direto para cima. Supondo que você não atire a pedra muito forte, ela subirá por algum tempo, mas eventualmente a aceleração devida à gravidade do planeta vai fazê-la descer de novo. Se você atirar a pedra com força suficiente, no entanto, você poderia fazê-la escapar inteiramente da gravidade do planeta. A pedra continuaria a subir para sempre. A velocidade com que é necessário atirar a pedra para que ela escape da atração gravitacional do planeta é chamada de "velocidade de escape". Como seria de esperar, a velocidade de escape depende da massa do planeta: se o planeta for extremamente massivo, sua gravidade é muito intensa, e a velocidade de escape muito elevada. Um planeta mais "leve" teria uma velocidade de escape inferior. A velocidade de escape também depende da distância a que você se encontra do centro do planeta: quanto mais perto você estiver, maior a velocidade de escape. A velocidade de escape da Terra é de 11,2 km/s (cerca de 40.000 km/h), enquanto que a velocidade de escape da Lua é de apenas 2,4 km/s (cerca de 8.600 km/h).
Imagine agora um objeto com tamanha massa, concentrada num raio de tal forma pequeno, que sua velocidade de escape seja maior que a velocidade da luz. Neste caso, uma vez que nada pode se deslocar mais rapidamente que a luz, nada poderá escapar do campo gravitacional desse objeto. Mesmo um raio de luz seria puxado de volta pela gravidade e não teria como escapar.
A ideia de uma concentração de massa tão densa que até mesmo a luz ficasse aprisionada vai bem ao passado, até Laplace, no século 18. Quase imediatamente em seguida de Einstein ter desenvolvido a relatividade geral, Karl Schwarzschild descobriu uma solução matemática para as equações daquela teoria que descreviam um tal objeto. Foi somente muito mais tarde, com o trabalho de cientistas como Oppenheimer (o mesmo do Projeto Manhattam, da bomba atômica americana), Volkoff e Snyder, na década de 30, que se começou a pensar seriamente na possibilidade de que tais objetos pudessem realmente existir no Universo. Esses pesquisadores mostraram que, quando uma estrela suficientemente massiva consome todo seu combustível, ela perde a capacidade de sustentar o encolhimento devido à sua própria atração gravitacional, e então desaba sobre si própria na forma de um buraco negro.
Na relatividade geral, a gravidade é uma manifestação da curvatura do espaço-tempo. objetos massivos distorcem as dimensões de espaço e tempo de tal forma que as regras normais da geometria não se aplicam mais. Perto de um buraco negro essa distorção do espaço é extremamente intensa, provocando o aparecimento de certas propriedades muito estranhas. Em particular, um buraco negro tem algo que se chama "horizonte de eventos", que é uma superfície esférica que marca as fronteiras do buraco negro. Você pode passar através do horizonte de eventos no sentido de entrada, mas depois não pode sair mais. Na verdade, uma vez cruzado o horizonte de eventos, você está inexoravelmente fadado a se aproximar cada vez mais da "singularidade" localizada no centro do buraco negro.
Você pode pensar no horizonte de eventos como um lugar em que a velocidade de escape é igual à velocidade da luz. Fora do horizonte de eventos, a velocidade de escape é menor do que a da luz, de modo que se você acionar seus foguetes com força suficiente poderá obter a energia necessária para escapar do buraco negro. Mas se você se encontrar para dentro do horizonte de eventos, não importa quão potentes sejam seus foguetes, pois você não poderá escapar.
O horizonte tem algumas propriedades geométricas realmente estranhas. Para um observador que esteja imóvel a alguma distância do buraco negro, o horizonte parece ser uma superfície esférica tranquila e estática. Mas à medida que você se aproximar do horizonte, perceberá que ele está se movendo a uma velocidade espantosa. Na verdade, está se expandindo à velocidade da luz! Isto explica porque é tão fácil atravessar o horizonte na direção para dentro, mas impossível retornar. Como o horizonte está se movendo à velocidade da luz, para poder escapar de volta através dele você teria que viajar a uma velocidade superior à da luz. Como você não poder viajar mais rápido do que a luz, você não pode escapar do buraco negro.
(Se toda esta história estiver soando muito estranha, não se preocupe. Ela é estranha. O horizonte é estático, num certo sentido, mas noutro sentido está se deslocando à velocidade da luz. É um pouco como aquela história de Alice no País das Maravilhas: ela tinha que correr tão rápido quanto possível, apenas para permanecer no mesmo lugar.)
Uma vez dentro do horizonte, o espaço-tempo é tão distorcido que as coordenadas que descrevem distância radial e tempo trocam suas posições. Ou seja, a coordenada que descreve a sua distância do centro, "r", passa a ser uma coordenada do tipo tempo, e a coordenada "t" passa a ser do tipo espacial. Uma consequência disto é que você não consegue mais evitar seu deslocamento no sentido de valores cada vez menores de r, da mesma forma como normalmente você não consegue evitar o deslocamento da coordenada de tempo na direção do futuro (ou seja, no sentido de valores maiores de t). Eventualmente você vai atingir a singularidade, localizada em r=0. Você pode tentar evitá-la acionando seus foguetes, mas é inútil: não importa qual a direção em que você tente fugir, não conseguirá evitar seu futuro. Tentar evitar o centro de um buraco negro depois de ter atravessado seu horizonte é como tentar evitar a próxima segunda-feira.
Por falar nisso, o nome "buraco negro" foi inventado por John Archibald Wheeler, e parece ter ficado mesmo por ser muito mais atraente dos que os anteriores. Antes de Wheeler aparecer, esses objetos eram conhecidos como "estrelas congeladas". A explicação está adiante.
[P] Qual é o tamanho de um buraco negro?
Há pelo menos duas maneiras diferentes de descrever o tamanho de alguma coisa. Podemos especificar que massa essa coisa tem, ou podemos especificar o espaço que ela ocupa. Primeiramente, vamos falar da massa dos buracos negros.
Em princípio, não existe limite nem superior nem inferior para a massa de um buraco negro. Qualquer quantidade de matéria pode, em teoria, se transformar num buraco negro, se for comprimida a uma densidade suficiente. Suspeita-se que a maioria dos buracos negros existentes no Universo tenham sido criados na morte de estrelas massivas, e por isso calcula-se que sua massa seja igual à dessas estrelas. A massa típica de um desses buracos negros estelares seria da ordem de 10 vezes a massa do Sol, ou cerca de 10^{31} quilogramas. (Aqui está sendo usada a notação científica:10^{31} significa 1 seguido de 31 zeros, ou 10,000,000,000,000,000,000,000,000,000,000.) Os astrônomos também suspeitam que muitas galáxias abriguem buracos negros extremamente massivos em seus centros. Esses buracos negros teriam massas um milhão de vezes maiores que a do Sol, ou 10^{36} quilogramas.
Quanto mais massivo for um buraco negro, mais espaço ele ocupa. Na verdade, o raio de Schwarzschild (que representa o raio do horizonte de eventos) e a massa são diretamente proporcionais: se um buraco negro tem massa dez vezes superior à de um outro, seu raio é dez vezes maior. Um buraco negro com massa igual à do Sol teria um raio de 3 quilômetros. Assim, um buraco negro típico com 10 massas solares teria um raio de 30 quilômetros, e um buraco negro de centro de galáxia com um milhão de massas solares teria um raio de 3 milhões de quilômetros. Este tamanho pode parecer muito grande, mas não o é em termos astronômicos. O Sol, por exemplo, tem um raio de cerca de 700.000 km, e assim um tal buraco negro supermassivo teria um raio apenas cerca de quatro vezes maior que o Sol.
[P] O que me aconteceria se eu caísse num buraco negro?
Suponhamos que você entre em sua nave espacial e a dirija para o buraco negro com um milhão de massas solares localizado no centro da nossa galáxia. (Na verdade, há algum debate sobre se a nossa galáxia contém ou não um buraco negro no seu centro, mas vamos supor que por ora isso seja verdade.) A uma longa distância do buraco negro, você simplesmente desliga seus motores e deixa a nave deslizar na direção dele. O que acontece?
A princípio, você não sente nenhuma força gravitacional. Uma vez que você está em queda livre, todas as partes do seu corpo, e mais todas as partes da nave, estão sendo puxadas da mesma forma, e portanto você tem a sensação de ausência de peso. (Isto é exatamente o que se passa com astronautas em órbita da Terra: mesmo que tanto os astronautas quanto a nave estejam sendo puxados pela gravidade da Terra, eles não sentem nenhuma força gravitacional, porque tudo está sendo puxado exatamente na mesma proporção.) À medida que você se aproxima cada vez mais do buraco negro, no entanto, você começa a sentir forças gravitacionais do tipo "de maré". Imagine que seus pés estejam mais próximos do centro do buraco negro do que sua cabeça (como se você estivesse caindo "em pé"). O puxão gravitacional fica mais intenso quanto mais você se aproxima do buraco negro, de forma que seus pés sentem uma força mais intensa do que sua cabeça. Como resultado, você se sente "esticado". (Esta força é chamada de força "de maré" porque é exatamente esse tipo de força que causa as marés na Terra.) Estas forças de maré ficam mais intensas à medida que você se aproxima do centro do buraco negro, e eventualmente você será feito em pedaços por elas.
Para um buraco negro de grandes dimensões como aquele onde você está caindo, as forças de maré só são perceptíveis a partir de 600.000 km de distância do centro. Atenção ao fato de que, neste caso, esta distância está já para dentro do horizonte de eventos. Se você estivesse caindo num buraco negro menor, digamos um com a mesma massa do Sol, as forças de maré seriam perceptíveis a cerca de 6.000 km de distância do centro, e portanto você seria desfeito muito antes de cruzar o horizonte de eventos desse buraco. (Essa é a razão porque imaginamos que o buraco negro do exemplo deveria ser grande, em vez de pequeno: para que você sobreviva pelo menos até cruzar o horizonte de eventos.)
O que é que você vê à medida que cai? Por surpreendente que pareça, nada de muito interessante será visto, necessariamente. As imagens dos objetos distantes podem ficar distorcidas de maneiras estranhas, uma vez que a gravidade do buraco negro desvia a luz, mas não muito mais do que isso. Em particular, nada de especial acontece no momento em que você cruza o horizonte de eventos. Mesmo depois de cruzá-lo, você continua a ver objetos do lado de fora: afinal, a luz proveniente deles ainda pode chegar até você. Ninguém do lado de fora, no entanto, poderá vê-lo, naturalmente, já que a luz de dentro não consegue escapar para fora do horizonte.
Quanto tempo dura todo o processo? Bem, é claro que isso depende da distância a que você estava quando começou. Digamos que se partisse do repouso num ponto situado a uma distância da singularidade igual a dez vezes o raio do buraco negro. Neste caso, para um buraco com um milhão de massas solares, você levaria cerca de 8 minutos para atingir o horizonte. Depois de atingido esse ponto, em apenas sete segundos você atingirá a singularidade! Como essas contas são diretamente proporcionais ao tamanho do buraco negro, se você estivesse se dirigindo a um buraco negro muito menor, morreria muito mais depressa.
Uma vez cruzado o horizonte, nos sete segundos restantes você poderia entrar em pânico e acionar seus foguetes, numa tentativa desesperada de evitar a singularidade. Infelizmente isso é inútil, pois a singularidade está localizada no seu futuro (variável t crescente), e é impossível evitar o seu futuro. Na verdade, quanto mais os foguetes forem acionados, tanto mais depressa você se dirigirá para a singularidade. A melhor (e única) coisa a fazer é apreciar a viagem.
[P] Minha amiga está a uma distância segura, observando minha queda em direção ao buraco negro. O que ela vê?
Ela vê as coisas de forma muito diferente que você. À medida que você se aproxima do horizonte, ela o vê mover-se cada vez mais devagar. Na verdade, independentemente de quanto tempo ela esperar, nunca o verá atingir precisamente o horizonte.
Isto é mais ou menos a mesma coisa que se pode dizer sobre o material do qual o buraco negro foi formado inicialmente. Suponha que o buraco negro se formou a partir do colapso de uma estrela. À medida que a estrela que vai formar o buraco negro entra em colapso, sua amiga a vê cada vez menor, aproximando-se mas nunca chegando ao seu raio de Schwarzschild. É por esta razão que os buracos negros originalmente eram chamados de estrelas congeladas: porque pareciam se "congelar" num tamanho um pouco apenas maior do que o raio de Schwarzschild.
Porquê ela vê as coisas dessa maneira? Talvez a melhor explicação seja que se trata de uma ilusão de óptica. O buraco negro não leva um tempo infinito para se formar, assim como você não leva um tempo infinito para cruzar o horizonte de eventos. (Se não acredita, tente você mesmo! Você estará do outro lado do horizonte em oito minutos, e morto esmagado em uns poucos segundos a mais.) À medida que você se aproxima do horizonte, a luz emitida por você levará cada vez mais tempo para chegar até a sua amiga. Com efeito, a luz que for emitida no momento exato em que você cruzar o horizonte ficará suspensa eternamente no horizonte, e nunca chegará até a sua amiga. Muito tempo pode já se ter passado depois de você cruzar o horizonte (e possivelmente morrido), os sinais luminosos emitidos por você que seriam a evidência daquele fato nunca chegarão à sua amiga.
Há uma outra forma de encarar toda esta questão. Num certo sentido, o tempo realmente passa mais devagar perto do horizonte do que longe dele. Suponha que você leve sua espaçonave até um ponto muito próximo do horizonte, e permaneça ali estacionado por algum tempo (queimando uma quantidade enorme de combustível para evitar cair no buraco negro). Depois, você retorna e se encontra de novo com sua amiga. Você descobrirá que ela envelheceu muito mais do que você durante todo o processo; o tempo passou mais devagar para você do que para ela.
Então, qual destas duas explicações (a da ilusão de óptica e a da desaceleração do tempo) é realmente a carreta? A resposta depende do sistema de coordenadas que for usado para descrever o buraco negro. Segundo o sistema usual de coordenadas, chamado de "coordenadas de Schwarzschild", você cruza o horizonte de eventos quando a coordenada de tempo t tiver valor infinito. Portanto, nestas coordenadas realmente o tempo gasto para cruzar o horizonte de eventos é infinito. Mas a razão para isso é que as coordenadas de Schwarzschild oferecem uma visão muito distorcida do que está acontecendo no horizonte, ou próximo dele. De fato, no próprio horizonte as coordenadas estão infinitamente distorcidas (ou, para usar a terminologia apropriada, são "singulares"). Se você escolher um sistema de coordenadas que não sejam singulares no horizonte, então você verá que o tempo ao cruzar o horizonte é realmente finito, mas o tempo em que sua amiga vê você a cruzar o horizonte é infinito, pois a radiação levou um tempo infinito para chegar até ela. No fundo, é permitido usar qualquer dos sistemas de coordenadas, e portanto ambas as explicações são válidas. São apenas maneiras diferentes de dizer a mesma coisa.
Na prática, você vai efetivamente se tornar invisível à sua amiga bem rapidamente, pela simples razão de que a luz emitida por você vai sofrer desvios para o vermelho à medida que se afasta do buraco negro. A luz que você emitir num certo comprimento de onda será vista por sua amiga com um comprimento de onda maior. Os comprimentos de onda vão se tornando cada vez maiores à medida que você se aproxima do horizonte. Eventualmente, você simplesmente deixará de ser visível: a luz emitida estará desviada para o infravermelho, depois para ondas de rádio. A partir de um certo ponto, os comprimentos de onda serão tão grandes que ela deixará de poder observá-los. Além disso, lembre-se que a luz é emitida em pacotes individuais chamados fótons. Suponha que você esteja emitindo fótons ao atravessar o horizonte. Num certo ponto, você emitirá o último fóton antes de cruzar o horizonte. Aquele fóton vai chegar à sua amiga num tempo finito - tipicamente menos de uma hora para um buraco negro de um milhão de massas solares - e depois disso ela nunca mais verá nada de você (afinal, nenhum dos fótons emitidos por você depois de cruzar o horizonte jamais chegarão a ela).
[P] Se um buraco negro existisse, ele terminaria por sugar toda a matéria do Universo?
De jeito nenhum. Um buraco negro tem um "horizonte", que significa uma região da qual você não pode escapar. Se você cruzar o horizonte, está fadado a eventualmente atingir a singularidade. Mas se você ficar longe do horizonte, você pode perfeitamente evitar ser sugado para dentro do buraco negro. Na verdade, para alguém a uma distância muito grande do horizonte, o campo gravitacional estabelecido por um buraco negro não tem nenhuma diferença do campo gravitacional estabelecido por qualquer outro objeto com a mesma massa. Em outras palavras, um buraco negro de uma massa solar não tem diferença nenhuma de qualquer outro objeto com uma massa solar (como por exemplo o próprio Sol), no que diz respeito à capacidade de "sugar" objetos distantes.
[P] E se o Sol se tornasse num buraco negro?
Bem, em primeiro lugar, deixe-me assegurar-lhe que o Sol não tem nenhuma intenção de o fazer. Somente estrelas com massa consideravelmente superior à do Sol terminam suas vidas como buracos negros. O Sol vai permanecer mais ou menos como está por ainda uns cinco bilhões de anos. Em seguida, vai passar por uma rápida fase como uma estrela gigante vermelhe, durante a qual vai se expandir até englobar as órbitas (e os próprios planetas) de Mercúrio e Vênus, e ainda tornar a vida na Terra bastante desconfortável (oceanos em fervura, atmosfera escapando para o espaço, coisas assim). Depois disso, o Sol vai terminar a vida como uma mera estrela anã branca. Se eu fosse você, faria planos de mudança para algum lugar muito distante antes que qualquer dessas coisas aconteça. Ah, e também não compraria nenhum daqueles títulos do governo resgatáveis em 8 bilhões de anos.
Mas voltemos ao assunto. E se o Sol se tornasse mesmo um buraco negro por alguma razão? O efeito principal seria que tudo ficaria muito escuro e frio por aqui. A Terra e os outros planetas não seriam sugados para o buraco negro; ficariam, isto sim, exatamente nas mesmas órbitas em que hoje estão. Porquê? Porque o horizonte do buraco negro seria muito pequeno - apenas uns 3 km - e, como observamos acima, desde que você fique longe do horizonte eventual, a gravidade do buraco negro não tem diferença daquela de qualquer outro objeto de mesma massa.
[P] Existe alguma evidência de que os buracos negros realmente existam?
Sim. Você não pode ver um buraco negro diretamente, claro, pois a luz não sai do seu horizonte de eventos. Isto quer dizer que temos que confiar em evidências indiretas da existência de buracos negros.
Suponha que você tenha encontrado uma região do espaço onde você pense que possa haver um buraco negro. Como é que se pode verificar se ele está mesmo lá? A primeira coisa a medir seria a massa existente na tal região. Se você encontrou uma massa muito grande concentrada num volume muito pequeno de espaço, e se a massa é escura, então as chances são boas de você ter encontrado mesmo um buraco negro. Existem dois tipos de sistemas onde os astrônomos encontraram objetos desse gênero, massivos, compactos e escuros: o centro das galáxias (inclusive, talvez, a nossa própria Via Láctea), e sistemas binários emissores de raios X na nossa galáxia.
Várias galáxias já foram detectadas como candidatas por conterem objetos massivos e escuros nos seus centros. As massas dos núcleos dessas galáxias vão de um milhão a vários bilhões de massas solares. Essas massas são medidas pela observação das velocidades orbitais das estrelas e do gás interestelar em torno do núcleo da galáxia: quanto maior a velocidade, maior a força gravitacional necessária para manter as estrelas e o gás nas suas órbitas. (Esta é a forma mais comum de medir massas em astronomia. Por exemplo, medimos a massa do Sol pela observação da velocidade dos planetas em órbita dele, e medimos a quantidade de matéria escura nas galáxias medindo a velocidade orbital de objetos nos limites da galáxia.)
Pensa-se que esses objetos escuros nos núcleos galácticos sejam buracos negros por pelo menos duas razões. Primeiro, é difícil pensar em qualquer outra coisa que eles pudessem ser: são muito densos e escuros para serem estrelas ou agrupamentos de estrelas. Segundo, a única teoria razoável na explicação dos objetos enigmáticos conhecidos como quasares (do inglês quasar, "quasi-stellar objects", objetos quase-estelares) e das galáxias ativas postula que tais galáxias contêm buracos negros supermassivos em seus núcleos. Se esta teoria estiver carreta, então uma fração significativa das galáxias - todas as que hoje são ou já foram ativas - devem ter buracos negros supermassivos em seus núcleos. Tomados em conjunto, estes argumentos sugerem fortemente que os núcleos destas galáxias contêm buracos negros, mas não constituem prova absoluta.
Duas descobertas muito recentes suportam ainda mais fortemente a hipótese acima. Primeiro, descobriu-se uma galáxia ativa próxima que contém um maser de água (um amplificador natural de radiação de microondas baseado em moléculas de água; o termo maser vem do inglês "Microwave Amplification by Stimulated Emission of Radiation") próximo do seu núcleo. Usando a técnica de interferometria de linha de base muito longa, um grupo de pesquisadores conseguiu determinar a distribuição de velocidades no gás com resolução muito fina. Com efeito, foram capazes de medir a velocidade a uma distância menor do que meio ano-luz do núcleo da galáxia. A partir dessas medidas, puderam concluir que objeto massivo no centro dessa galáxia tem menos do que meio ano luz de raio. É difícil imaginar qualquer outra coisa a não ser um buraco negro que tenha tanta massa concentrada num volume tão pequeno. (Esses resultados foram apresentados no volume 373, pág. 127, da edição da revista Nature de 13 de Janeiro de 1995.)
Uma segunda descoberta oferece prova ainda mais conclusiva. astrônomos de raios X detectaram uma linha espectral de um núcleo galáctico que indica a presença de átomos perto do núcleo que se movem a uma velocidade muito elevada (cerca de um terço da velocidade da luz). Além disso, a radiação desses átomos foi desviada para o vermelho exatamente da mesma maneira prevista para a radiação emitida das proximidades do horizonte de eventos de um buraco negro. Seria muito difícil explicar isso de qualquer outra forma a não ser com um buraco negro e, se estas descobertas forem comprovadas, então a hipótese de que alguns núcleos galácticos contêm buracos negros supermassivos estaria praticamente assegurada. (Estes resultados foram apresentados no volume 375, pág. 659, da edição da revista Nature de 22 de Junho de 1995.)
Uma classe completamente diferente de candidatos a buracos negros pode ser encontrada na nossa própria galáxia. Trata-se de buracos negros muito menores, de massas de ordem estelar, que pensa-se que sejam formados quando uma estrela massiva termina sua vida numa explosão de supernova. Se um tal buraco negro estelar estivesse sozinho por aí, não teríamos muita chance de achá-lo. Entretanto, muitas estrelas existem na forma de sistemas binários - pares de estrelas uma em órbita da outra. Se uma das estrelas num tal sistema binário se tornar um buraco negro, poderíamos detectá-lo. Em particular, em alguns sistemas binários contendo um objeto compacto como um buraco negro a matéria do outro objeto é sugada e forma um assim chamado "disco de acreção" que fica girando em torno e caindo na direção do buraco negro. A matéria do disco de acreção fica muito aquecida à medida que cai para o buraco negro, emitindo intensas quantidades de radiação, na sua maior parte na faixa do espectro correspondente aos raios X. Muitos desses "sistemas binários de raios X" são conhecidos, e pensa-se que alguns sejam fortes candidatos a buracos negros.
Suponha que você tenha encontrado um sistema binário de raios X. Como pode saber se o objeto não visível é mesmo um buraco negro? Uma das coisas certamente necessárias de estimar é a massa do objeto. Através da medida da velocidade orbital da estrela visível (junto com mais outros parâmetros), pode-se deduzir a massa da companheira invisível. (A técnica é muito semelhante àquela descrita acima para buracos negros supermassivos em núcleos galácticos: quanto mais rápido a estrela se mover, maior a força gravitacional necessária para mantê-la na órbita, e portanto mais massa tem a companheira invisível.) Se se concluir que a massa do objeto compacto é muito, muito grande, entra novamente em cena o argumento de não se conhecer outro objeto que pudesse ser senão um buraco negro. (Uma estrela normal com a mesma massa seria visível. Os restos de uma estrela tal como uma estrela de nêutrons não seriam capazes de impedir o próprio encolhimento gravitacional, e entrariam em colapso até formar um buraco negro.) A combinação dessas estimativas de massa com estudos detalhados da radiação do disco de acresção pode fornecer evidência circunstancial suficiente para decidir que o objeto em questão é mesmo um buraco negro.
Muitos desses sistemas binários de raios X são hoje conhecidos, e em alguns casos a evidência a favor da hipótese dos buracos negros é bastante forte. Num artigo publicado na edição de 1992 da Revista Anual de Astronomia e Astrofísica, Anne Cowley resumiu a situação dizendo que havia três sistemas conhecidos na altura (dois na nossa galáxia e um na vizinha Grande Nuvem de Magalhães) para os quais existe evidência muito forte de que a massa do objeto invisível é grande demais para ser qualquer outra coisa que não seja um buraco negro. Existem muitos outros objetos que se pensa sejam buracos negros com apoio em evidência menos convincente. Além disso, este campo de pesquisa tem estado muito ativo desde 1992, e o número de candidatos fortes atualmente é muito maior que três.